Unemployment line? No, but close enough

UPDATE 7:27 pm GMT, April 18: reader Rhett Schexnaydre pointed out that we put a decimal point in the wrong place. We fixed it. Women are right: math is hard!

Last week we good-naturedly ragged on the brilliant PKamp3 at DQYDJ.net (it stands for Don’t Quit Your Day Job). He threw away his usually tight rationality for an afternoon so he could buy…Mega Millions tickets. $60 worth, no less. Best of all, he then blamed it on his wife.

It’s not like PKamp3 was without company. 1.5 billion Mega Millions tickets were sold for the recent record-breaking jackpot. That’s 5 tickets per American, maybe 7 or 8 per American adult. We’d love to know how many people bought tickets (or equivalently, how many tickets the average player bought.) Alas, we can only guess. But at least some smart people are buying 60 tickets at once. Other, less smart people are making 70-mile excursions to wait in line for 4 hours to buy tickets, and it’s probably safe to assume that an irrational lottery ticket buyer isn’t going to burn 5+ hours and maybe $13 worth of gas to buy just a solitary $1 ticket.

The record $462 million Mega Millions jackpot came and went, and today a meager and pathetic $30 million jackpot sits in its place. Clearly $30 million isn’t enough to change the lives of any of the myriads of people who bought tickets for the record jackpot, but are sitting this week’s drawing out.

The point of this post isn’t to decry lottery ticket buyers. We’ve done that repeatedly on this site. Rather it’s to answer what was then a rhetorical question in last week’s Carnival of Wealth – what does the mean lottery prize look like, vis-à-vis the median prize?

Obviously, the expected value of a $1 ticket is somewhere south of $1. But is that enough to say it’s a bad investment?

Say the expected value of a ticket was, for some reason, 10.2 times its price. Maybe whoever’s running the lottery is feeling particularly eleemosynary. By simple measures, an average return of 1020% means that you should invest all your money in lottery tickets. In the long run, you couldn’t help but win.

Okay, but what if that lottery worked as follows?

-only 100 tickets are sold.
-1 ticket wins $102 million.
-99 tickets lose.
-each ticket costs $100,000.

Hold on, soldier. Even though the “expected” value of your ticket is $1,020,000, no one expects to win exactly that much. You’re either going to win $102 million, or nothing. (Keep in mind that winning “nothing” means losing $100,000.)

You can’t just add up the prizes and divide by the tickets sold to estimate how much you’ll win or lose. You have to look at how often particular prizes occur.

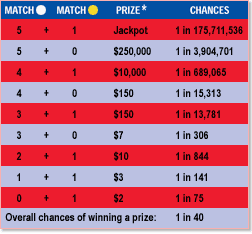
So say you bought 175,711,736 tickets for the aforementioned $30 million Mega Millions drawing. In other words, you covered every combination. You’d guarantee yourself a share of the jackpot, but how big a share (and what else)?

45 of those tickets will each win a quarter million. So that’s $11,250,000.

255 tickets will each win $10,000. Another $2,550,000.

24,225 tickets will each win $150. Add $3,633,750 to our pot.

208,250 tickets will each win $10, for $2,082,500.

573,750 tickets will each win $7, another $4,016,250.

We’re almost done. Sorry this is so boring. Go ahead and attempt to plow through The Simple Dollar’s latest, and you’ll appreciate how riveting a post this is.

1,249,500 $3 winners total $3,748,500, and 2,349,060 $2 winners add up to $4,698,120.

Cumulative total, $31,979,120 plus the variable jackpot. Call it $30 million, making our total $61,979,120.

Cumulative number of winners? 4,405,086. Remember how many tickets you need to cover the bases? See above.

97.5% of tickets are losers. By extension, 97.5% of lottery players are…well, we don’t call people losers on this site. Retards, maybe. If you finished in the 97th percentile of players, your ticket would return you a payment of 0.

This applies with regard to real investments, too. The science of investment advice hasn’t yet progressed to the point where advisors disclose the likelihood of receiving a particular payout for a stock, although it’d be awesome if they did. (“Your Sprint Nextel stock has a 4.2% chance of closing above $5 by year-end, an 11.9% chance of reaching at least $4, a 43.2% chance of falling below $2, etc.”)

(NB: Why can’t we do this? We have markets for everything from sports wagering to political races. But among securities, we do this for commodities only. Anybody know why we don’t extend it to other investments? That’s a sincere question, not a rhetorical one.)

That being said, the likelihood of a payout is every bit as important as the magnitude of the payout. You can’t explain that concept to someone who plays the lottery every week, or even to someone who’s proud that he has a “system” for winning at blackjack, but the idea is beyond critical for every successful investor. Even if the investment itself is
modest. (If you spend $30,000 on a taco truck, at 4.9% financing, then spend another $5000 modifying it to incorporate a mobile kitchen, not to mention $20 a day in gas, what’s the likelihood of you selling enough tacos to enjoy a 10% annual profit margin? Or a 50% one? If that’s the business you happen to be in, those questions aren’t rhetorical either.)

One thing’s certain, though. Almost any real business you choose to invest in is going to have less than a 97.5% chance of wiping out your investment.

This article is featured in:

**Totally Money Blog Carnival-Big Bang Theory Birthday Edition**